 licenciado sob uma Licença Creative Commons.
licenciado sob uma Licença Creative Commons.MIA> Biblioteca> Ernst Kolman > Novidades
Primeira Edição: 1931
Fonte: Ciência na Encruzilhada: Documentos apresentados ao Congresso Internacional de História da Ciência e Tecnica Realizado em Londres de 29 de junho a 3 de julho de 1931 pelos delegados da URSS, Frank Cass and Co., 1931;
Tradução: Reinaldo Pedreira Cerqueira da Silva
HTML: Fernando Araújo.
Direitos de Reprodução:  licenciado sob uma Licença Creative Commons.
licenciado sob uma Licença Creative Commons.
A posição da matemática, como a de qualquer ciência, é no fundo determinada pelo desenvolvimento e posição das forças de produção, de tecnologia e economia. Estes últimos afetam diretamente a matemática, apresentando-a com novos problemas, criando sua base material e fornecendo sua força de trabalho e, indiretamente, através da visão predominante sobre o mundo, a filosofia da classe dominante.
Assim, se quisermos lidar com a atual crise das ciências matemáticas, devemos levar em consideração a crise na ciência burguesa como um todo, a crise nas ciências naturais burguesas e, particularmente, na física. O presente artigo, no entanto, não pretende reivindicar completamente este aspecto do problema apresentado, a conexão entre a crise da matemática e a crise geral na ciência burguesa, bem como sua conexão com toda a crise dentro do capitalismo como um todo. É suficiente indicar que a crise que hoje está perturbando toda a ciência burguesa representa uma nova e mais alta fase dessa crise, experimentada pela física e pela química desde a abertura do século XX, que Lenin analisou com a mente de uma gênio em sua obra, publicado em 1908 Materialismo e Empirio-Críticismo.
Do complexo inteiro relevante de problemas, um é de especial interesse para nós hoje: a crise na matemática tomada em si mesma. Sua importância é extremamente grande; pois não há dúvida de que, como a crise das ciências naturais afeta a matemática, a crise da matemática, por sua vez, exerce influência sobre a física, a química e a tecnica. Sobre a posição da matemática, sobre a sua capacidade de resolver este ou aquele problema, depende em grande medida a possibilidade de um maior desenvolvimento das ciências naturais e da tecnica.
Isso se aplica com particular força à física atual, com seu aparato matemático extraordinariamente abundante, com seus esforços para formalizar a física, para geometrizá-la, seu objetivo de permitir que a matéria desapareça e reter somente as equações - as tendências tão surpreendentemente reveladas por Lênin. . A matemática da física assusta o próprio físico; Assim, por exemplo, falando de matemática na física, Khvolson diz: "A coisa mais terrível é que essa matemática não é a matemática ensinada na universidade. Nem um único físico ouviu nada sobre a última. A coisa mais terrível é , que sua importância está crescendo continuamente ". E apesar de nos opormos a tal obscurantismo, devemos admitir que a física está se tornando cada vez mais dependente do destino da matemática.
É extremamente característico que essa matemática especial - a análise do tensor, o cálculo matricial, a teoria dos números característicos - tenha, em grande parte, sido criada pelos próprios físicos, pois a matemática comum é incapaz de satisfazer as exigências da física atual. .
A análise, o instrumento mais poderoso da matemática, desenvolveu-se no solo proporcionado pelas ciências naturais, a física e a mecânica dos séculos XVII, XVIII e XIX; isto é, sobre o princípio da continuidade "natura non facit saltus". A mecânica e a termodinâmica fenomenológica consideravam todos os processos como contínuos (pelo menos em uma primeira aproximação) e os expressavam analiticamente. O mesmo aconteceu com o eletromagnetismo e até com a química.
No entanto, uma série de descobertas foram forçadas a essa "harmonia de continuidade", que, começando com o quantum de energia de Planck necessário para explicar a radiação de calor de um corpo negro, se desenvolve através de quanta de luz e fótons para a mecânica das ondas. Broglie, Heisenberg e Schrodinger. A física não poderia fornecer nenhuma explicação analítica consistente para esses fenômenos e todas as tentativas de estabelecer uma síntese de ondas e átomos, de eletromagnetismo e gravitação, falharam até agora, ou na melhor das hipóteses, resultaram meramente em hipóteses ad hoc. Assim, por exemplo, a teoria unitária da eletricidade de Dirac, que é compelida a introduzir a concepção de energia negativa, apenas confirma novamente a afirmação de que a dialética, que está forçando seu caminho para a ciência com poder elementar, torna-se uma caricatura de si mesmo nas mãos de físicos idealistas. Ainda menos capacidade de trabalho é exibida pela matemática, que é pouco capaz de resolver as equações da mecânica das ondas nas instâncias mais simples e triviais.
Essa incapacidade de apresentar uma imagem adequada da realidade material - isto é, do mundo que existe independentemente de nossa consciência - é exibida na análise mesmo em instâncias comparativamente elementares.
Tomemos, por exemplo, um problema como o de resfriar uma vara, que parecerá bastante simples para qualquer pessoa que ainda não tenha sido corrompida pela física e pela matemática da escola. É bem conhecido, no entanto, que a solução da equação diferencial parcial relevante com as suas condições de contorno relevantes é de importância apenas se tivermos encontrado uma série de valores discretos de um parâmetro. Assim, em si mesma, a solução contínua da equação diferencial parcial não ajuda a elucidar a natureza física do fenômeno. A assistência é oferecida por uma série descontínua de números e a solução rompe os limites da continuidade.
Encontramos circunstâncias similares em problemas relacionados com o equilíbrio dos filmes (Plateau) e com todo o grupo de problemas em que o dado conjunto de circunstâncias depende de todas as circunstâncias precedentes, isto é, sempre que encontramos equações integrais, em numerosos problemas. É óbvio que isso consistindo de dois ramos totalmente separados, ao longo dos quais a análise é obrigada a buscar uma saída - primeiro por soluções contínuas e, segundo, por valores discretos - pode ser considerado apenas como provisório e paliativo. . É óbvio que novos caminhos devem ser buscados.
E de fato os matemáticos estão tentando encontrar uma nova estrada, mas não na direção certa. Ao contrário da análise, que é baseada na idéia de continuidade, o primeiro quarto do nosso século testemunhou o desenvolvimento vigoroso daquele ramo da matemática que atribui o primeiro lugar à idéia de descontinuidade como auto-suficiente - a teoria dos múltiplos , a teoria das funções reais e, na forma mais completa, a teoria das variedades analíticas.
Para não ir muito longe, gostaríamos de nos referir ao livro do acadêmico Lusin (Moscou) publicado em Paris em 1930: Lecons sur les ensembles analytiques et leurs applications.O princípio principal depende da formação do que é chamado de domínio fundamental de Bair. Todos os pontos com coordenadas racionais são excluídos do continuum, apenas os pontos restantes que possuem coordenadas irracionais; estes formam o domínio fundamental e várias operações são realizadas com eles. Isso nos dá uma descontinuidade absoluta, pois em um domínio pequeno de qualquer ponto de descontinuidade que você possa escolher, há tantos pontos de descontinuidade do contínuo original. Surge a pergunta: onde existe na natureza material algo para o qual tal descontinuidade absoluta seria adequada? Encontramos uma resposta inesperada para essa pergunta difícil na introdução de Lebesque ao livro mencionado acima: em sua opinião, o valor filosófico deste trabalho é ainda maior do que seu valor matemático, para seu ponto de vista é o ponto de vista do solipsismo. Não é difícil entender que as variedades analíticas que se constroem sobre o conceito de descontinuidade absoluta refletem com notável fidelidade o extremo individualismo da filosofia idealista.
Somos assim apresentados a dois extremos: a continuidade transformada em absoluta e a discreta feita absoluta, ambas reivindicando significado independente e único, nem buscando a unidade recíproca, cada uma dando uma imagem unilateral da realidade material. Consequentemente, o problema não se resolve rejeitando a análise e a matemática discreta como sendo irregulares e contrárias à lei, rejeitando as duas sem mais delongas, a fim de recomeçar a construção em terreno limpo; A solução está em criar uma nova forma de cálculo que, procedendo de um princípio uniforme, une em si os lados positivos da análise e da matemática discreta.
O método de criar um suplemento externo - da matemática discreta - à análise é, portanto, incapaz de fornecer a síntese de continuidade e descontinuidade; é incapaz de conduzir a matemática para fora de sua posição atual, na qual funções contendo descontinuidades são tratadas como "não razoáveis", nas quais as lacunas são consideradas como exceções revolucionárias indesejáveis e indesejáveis; ou, por outro lado, em que o discreto é feito absoluto e considerado como o conjunto de indivíduos isolados. Não precisamos de duas análises, mas uma que, em suas operações, refletisse a unidade contínua e descontínua. Mas para que tal unidade seja estabelecida, a matemática deve tornar-se dialética e os matemáticos não devem resistir ao materialismo dialético.
As tentativas de superar a crise na atual posição da matemática, que é incapaz de oferecer uma síntese de continuum e descontinuum, porque está nas mãos de matemáticos metafísicos, também podem ser descritas como tentativas de aritmetizar a análise. As tentativas são feitas com meios inadequados. O velho chamado de Kronecker: "De volta à aritmética!" é tão reacionário quanto o grito moderno para deixar a física voltar à magia, a química à alquimia e a medicina a Hipócrates. Não devemos aritmetizar a análise, mas introduzir uma nova qualidade e preencher o abismo entre a continuidade e a descontinuidade.
Além desse abismo, no entanto, não podemos deixar de chamar a atenção para um segundo, e isso é a brecha entre a matemática como um todo e o cálculo da probabilidade, que é de particular importância em relação ao papel da estatística na física atual. , biologia, etc.
O cálculo da probabilidade, como é bem conhecido, faz uso de todos os ramos da matemática: aritmética, álgebra e análise, mas não é nisso que reside a sua profunda conexão com a matemática como um todo.
Pela teoria da probabilidade geométrica sabe-se que é possível determinar experimentalmente o valor do número π jogando uma agulha sobre uma superfície quadraticamente pautada e contando o número de instâncias nas quais as linhas são cortadas pela agulha, como Buffon mostrou em 1777, em seu Essai d'arithmetque moral, e como foi praticamente demonstrado por Wolff em Zurique.
Do mesmo caráter que este problema, no qual é possível, por um grande número de experimentos, determinar com uma pequena margem de erro magnitudes matemáticas exatas, estão os bem conhecidos problemas de urna, como determinar a probabilidade de que, no desenho um número par de bolas de uma urna contendo um número igual de bolas pretas e brancas, as bolas pretas e brancas aparecerão em números iguais, em que a expressão de probabilidade contém a raiz quadrada de um π. Ou, como outro exemplo, a determinação da probabilidade de que, ao desenhar bolas numeradas isoladas de uma urna, o número da bola desenhada não coincida uma vez com o número de série, o que dá uma probabilidade de i / e no caso em que o número de bolas excede todos os limites. Pode parecer ainda mais surpreendente que o cálculo da probabilidade nos permita encontrar relações algébricas e aritméticas, muitas vezes extremamente complexas. Assim, por exemplo, o conhecido problema de Moivre, dado em sua obra "De mensura sortis seu probabilitate eventuum in ludis a casu fortuito pendetibus", publicado em 1711, consiste em encontrar a probabilidade de, no desenho de bolas numeradas, dos números será igual a um número dado anteriormente, leva à relação:
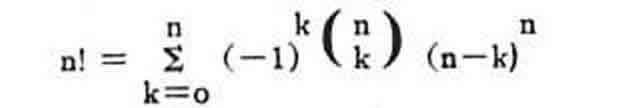
Ou, vamos tomar outro exemplo, bastante elementar, mas extremamente importante metodologicamente: o resumo de uma série geométrica por meio de um procedimento de probabilidade; este exemplo, ao mesmo tempo, propõe o problema de encontrar esquemas estocásticos que permitirão adicionar séries convergentes ainda mais complexas. Finalmente, nós também ressaltamos que o cálculo da probabilidade nos permite verificar com precisão suficiente que irracionais como √ 2, como indicado na mesma conexão, pelo professor Khotimsky (Moscou). Na verdade, se concedermos uma margem de erro de 0,5, chegamos a 2 √ 2 = √ 8 = 3, 5 √ 2 = √ 50 = 7, 7 √ 2 = √ 98 = 10 do qual se segue, na teoria dos erros , naquela
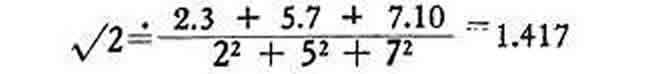
O problema geral de determinar com a precisão desejada as raízes de uma equação por métodos estocásticos pode ser colocado de maneira análoga.
Surge a questão de como tais resultados são possíveis. Como é possível que um cálculo baseado no acaso possa fornecer leis exatas, pode levar a resultados mais exatos? Esta questão não é respondida pela matemática atual: ela não estuda essas relações, mas as considera como uma espécie de curiosidade ou mistério, e é completamente incapaz de explicá-las, porque seu modo de pensamento metafísico é incapaz de compreender unidade de regularidade estatística e dinâmica, considerando-as como existindo separadamente e antagonisticamente. Essa circunstância, no entanto, não é apenas de significado filosófico; isso significa que a teoria estatística atual está paralisada, que a lei dos grandes números não é desenvolvida na direção de processos variados. Tudo isso, por sua vez, está ligado ao fato de que a matemática se desenvolveu principalmente com base nas ciências naturais e é inteiramente inadequada para atender às necessidades da economia política científica. Não é difícil entender por que todas as tentativas de estabelecer, ao longo de linhas puramente formais, uma correspondência entre os elementos do cálculo da probabilidade e da análise foram estéreis de resultado.
O terceiro, ainda mais amplo e profundo abismo na matemática atual, reside na extrema falta de qualidade na maioria de seus métodos. Por falta de qualidade em matemática, não queremos dizer, é claro, que os conceitos matemáticos tenham apenas que representar repetições de alguns conceitos principais, suas complicações quantitativas. Ao permanecer uma ciência de magnitude, a matemática cria em si mesma suas próprias qualidades matemáticas específicas. De fato, ela se desenvolve como um todo de quantidade para massa, do abstrato para o concreto e recebe novos conteúdos da influência da física e das ciências naturais em geral. No entanto, esse desenvolvimento é extremamente contraditório: nos ramos separados da matemática, muitas vezes procede do concreto a uma abstração cada vez maior, eliminando cada vez mais os fatores quantitativos. Um excelente exemplo é oferecido pelas geometrias não euclidianas. Enquanto, na verdade, sua origem reflete um conhecimento mais profundo da realidade, na matemática burguesa o fato de sua existência é usado como evidência conclusiva da correção do idealismo e até mesmo seu tratamento matemático sofre distorção idealista. Deste modo, aquilo que realmente forma o poder cognitivo da matemática, seu colossal poder de abstração em certos estágios de seu desenvolvimento, é transformado em sua própria contradição e torna a matemática de uma dada formação social incapaz de lidar com os problemas mais complicados que surgem como nosso conhecimento físico penetra mais profundamente na profundidade da matéria. E mesmo se não formos capazes de mudar radicalmente a natureza do objeto da matemática, uma vez que, pelo contrário, a matemática reflete a dependência real como dependência funcional; isto é, até mesmo a dependência mais simples, a causal, é aqui retratada da maneira mais distorcida e irrelevante; ainda menos a matemática pode retratar essa dependência como interação e a unidade de contradições mutuamente interpenetrantes. Equações matemáticas não têm direção, enquanto equações que não são despojadas das propriedades qualitativas da realidade - sejam elas equações da forma de valor na economia política ou equações químicas - possuem direção por sua própria natureza. Em "Capital", Marx refere-se à polaridade da forma simples de valor, em que a expressão
20 ells de linho é igual a 1 casaco
não pode ser simplesmente transposto para
1 casaco é igual a 20 ells de linho.
A irreversibilidade das equações químicas, que são exotérmicas em uma direção e endotérmicas na outra, é geralmente conhecida. Surge então a questão de por que os símbolos matemáticos e as operações com eles não poderiam se aproximar de muitas dessas peculiaridades qualitativas das quais a matemática, de outra forma, faria abstrações. Essa maneira de colocar a questão, no entanto, não tem nada em comum com as tentativas de matematizar todas as leis, nada em comum com as tentativas de dar uma visão pan-matemática do mundo, tentativas que dependem do pitagorismo e da cabalística. O objeto da matemática tem limites, assim como o objeto da física, da química, da biologia ou da economia política. Assim como as leis da economia política não podem ser investigadas pela biologia ou pela física, assim como a física e a química são incapazes de elucidar as leis biológicas, então a matemática nunca estará em condições de substituir a física, a química, etc. Mesmo que matemática, geometria, mecânica, física, química, biologia, etc., tenham muito em comum, todas elas tratam das leis das diferentes formas. do movimento da matéria, e enquanto, por exemplo, a física e a química, por um lado, e a biologia, por outro, não podem ser consideradas tão nitidamente separadas umas das outras quanto os vitalistas nos fazem crer, o materialismo dialético não adota o ponto de vista ingênuo. materialismo mecanicista, que reduziria a biologia à química e à física, estas à mecânica e o segundo à geometria e à matemática. Unidade implica identidade tão pouco quanto diferença implica separação. Mantendo sua física, química, biologia, etc., têm muito em comum, que todos eles tratam das leis das diferentes formas de movimento da matéria, e enquanto, por exemplo, física e química, por um lado, e biologia, por outro, não podem Como os vitalistas querem nos fazer crer, o materialismo dialético não adota o ponto de vista do materialismo mecanicista ingênuo, que reduziria a biologia à química e à física, à mecânica e a segunda à geometria e à matemática. Unidade implica identidade tão pouco quanto diferença implica separação. Mantendo sua física, química, biologia, etc., têm muito em comum, que todos eles tratam das leis das diferentes formas de movimento da matéria, e enquanto, por exemplo, física e química, por um lado, e biologia, por outro, não podem Como os vitalistas querem nos fazer crer, o materialismo dialético não adota o ponto de vista do materialismo mecanicista ingênuo, que reduziria a biologia à química e à física, à mecânica e a segunda à geometria e à matemática. Unidade implica identidade tão pouco quanto diferença implica separação. Mantendo sua física e química, por um lado, e biologia, por outro, não podem ser consideradas tão nitidamente separadas umas das outras quanto os vitalistas nos fazem crer, o materialismo dialético não adota o ponto de vista do materialismo mecanicista ingênuo, que reduziria a biologia à química e à física , estes para mecânica e o segundo para geometria e matemática. Unidade implica identidade tão pouco quanto diferença implica separação. Mantendo sua física e química, por um lado, e biologia, por outro, não podem ser consideradas tão nitidamente separadas umas das outras quanto os vitalistas nos fazem crer, o materialismo dialético não adota o ponto de vista do materialismo mecanicista ingênuo, que reduziria a biologia à química e à física , estes para mecânica e o segundo para geometria e matemática. Unidade implica identidade tão pouco quanto diferença implica separação. Mantendo suaspecificum e sem pretender ser uma panaceia, a matemática pode e deve, num determinado estágio de seu desenvolvimento, voltar ao ponto de partida, à maior concretude, a uma maior preocupação com a qualidade.
Este tipo de tentativa já foi feito com sucesso. Assim, por exemplo, tanto magnitude quanto direção figuram na análise vetorial, cuja origem e desenvolvimento estão intimamente ligados à história da mecânica e da eletromecânica. Por que não deveríamos prosseguir nesse caminho e tentar criar um novo cálculo qualitativo, por exemplo, para os propósitos de qualquer ramo da física? Por que não deveríamos, desse modo, colocar em funcionamento o grão de verdade contido na confusão idealista de Leibnitz, isto é, criar um cálculo que seria capaz de "representar figuras e até máquinas e movimentos por letras, apenas como álgebra representa números e magnitudes ". (Carta de Leibnitz a Huyghens, 1679).
O quarto principal abismo na matemática atual é aquele entre o histórico e o lógico. A matemática levanta problemas, opera com conceitos e métodos que são, obviamente, historicamente necessários, que são condicionados por todo o desenvolvimento da tecnologia, das ciências naturais, da filosofia e da própria matemática. Mas na própria matemática, como um sistema de ciência, essa necessidade histórica não é refletida diretamente. Tomemos como exemplo o desenvolvimento de um conceito tão fundamental como o do número.
Atualmente, a matemática desenvolve esse conceito com base no chamado princípio da permanência hankeliana ou no princípio axiomático de Hilbert. Mas o princípio da permanência nunca é realizado - o desenvolvimento do número rompe. Quanto à axiomática de Hilbert, é verdade que é útil para explicar as conexões lógicas entre os conceitos matemáticos individuais, mas, uma vez que ela representa uma construção pós-fato, ela também é incapaz de fornecer uma imagem correta do desenvolvimento. Assim, de fato, ambos os princípios apenas obscurecem o desenvolvimento histórico que realmente ocorreu.
Daríamos, como outro exemplo, uma expressão fundamental como é bem sabido que esta expressão não foi inventada artificialmente; surgiu das exigências históricas do comércio exterior, da necessidade de criar, para cálculos práticos, as tabelas logarítmicas mais adequadas. Portanto, a resposta à pergunta por que esse limite e e nenhum outro é tratado, não é dada pela matemática, mas pela história. Não obstante, há algum ponto em buscar as razões lógicas para as quais estudamos precisamente essa expressão limitante. Podemos também chegar à mesma questão por outra via: precisamos que expressões limitadoras análogas sejam construídas, de modo que o número eestá incluído como um link em tal série. É claro que o problema não é inequívoco, mas se houvesse tal série, nos ofereceria a possibilidade de obter uma compreensão mais completa do número e. Na verdade, Hilbert aborda esse problema a partir de outro aspecto: no 12º ponto de seu Programa de Paris, ele propõe o problema de encontrar funções que desempenhem a mesma função em qualquer corpo algébrico que a função exponencial desempenha para o corpo de números racionais.
Uma vez que, no sistema atual da matemática, não há razões lógicas para o tratamento de qualquer assunto dado, parece a qualquer um que não esteja familiarizado com a história da matemática que todas as novas idéias e todos os novos problemas aparecem esporadicamente na matemática, e apresentar problemas como os mencionados acima causa confusão entre os matemáticos, pois a matemática em sua posição atual não oferece pistas para sua solução. Esta circunstância é favorável ao idealismo, ao fideísmo,fazendo parecer que se trata da livre criação do entendimento imanente, da inspiração e, ao mesmo tempo, demonstra a incapacidade da matemática atual para fornecer generalizações de longo alcance que lhe dariam um poderoso impulso adiante, abraçar todos os seus ramos, eliminar o paralelismo existente e retirar dele estratificações geológicas supérfluas. Se isso for feito, o abismo entre o histórico e o lógico na estrutura matemática, métodos e problemática deve ser revisado à luz da unidade do histórico e do lógico.
O quinto abismo na matemática existe entre teoria e prática na própria matemática. Enquanto a teoria matemática é extremamente ramificada e se desenvolve muito rápida e luxuriantemente, a prática matemática, isto é, os métodos de cálculo, mal avança; na verdade, praticamente ficou parado na posição ocupada nos séculos XVII e XVIII. Na verdade, todo problema matemático, se é que tem algum significado na prática, deve eventualmente levar a algum processo de cálculo, a solução que a teoria matemática nos oferece deve ser eficaz. Como é, no entanto, a maior parte da matemática, e particularmente a mais recente, não nos dá resultados efetivos e dificilmente dificulta fazê-lo, preocupando-se mais com "provas da existência" lógicas.
Os métodos de cálculo que usamos podem, em essência, ser rastreados até os logaritmos usados por Newton. Um grande número de métodos matemáticos, poderosos na teoria, são provados na prática como inúteis porque as formas de sua aplicação não foram trabalhadas. Estes incluem todos os processos de autodesenvolvimento como, por exemplo, séries convergentes, produtos, frações contínuas, iterações, processos recorrentes, cuja lenta convergência os torna em grande parte inúteis. Uma vez que, na matemática atual como na ciência burguesa como um todo, a matemática "pura" é mantida totalmente à parte da matemática aplicada, a questão dos métodos de cálculo, instrumentos e tabelas que permitiriam categorias inteiras de séries convergentes de um determinado tipo. ser resumido com a precisão necessária - para dar um exemplo - não é sequer levantada, e em qualquer caso, a matemática "pura" considera que não tem qualquer influência sobre sua ciência divina. Não obstante, a criação de tais instrumentos nos daria novos logaritmos que nos permitiriam atacar problemas muito mais complicados do que podemos no presente, quando somos compelidos a considerar um problema como resolvido apenas quando conduz às operações aritméticas principais. Dessa forma, o problema da redução seria colocado sob uma nova luz. Mas, para preencher o abismo entre a teoria colossal e a eficácia comparativamente pequena da matemática, é essencial ter uma compreensão realmente científica da unidade da teoria e prática, uma compreensão da primazia da prática sobre a teoria que a matemática burguesa adota. dia não, e não pode possuir. a matemática considera que não tem qualquer influência sobre sua ciência divina. Não obstante, a criação de tais instrumentos nos daria novos logaritmos que nos permitiriam atacar problemas muito mais complicados do que podemos no presente, quando somos compelidos a considerar um problema como resolvido apenas quando conduz às operações aritméticas principais. Dessa forma, o problema da redução seria colocado sob uma nova luz. Mas, para preencher o abismo entre a teoria colossal e a eficácia comparativamente pequena da matemática, é essencial ter uma compreensão realmente científica da unidade da teoria e prática, uma compreensão da primazia da prática sobre a teoria que a matemática burguesa adota. dia não, e não pode possuir. a matemática considera que não tem qualquer influência sobre sua ciência divina. Não obstante, a criação de tais instrumentos nos daria novos logaritmos que nos permitiriam atacar problemas muito mais complicados do que podemos no presente, quando somos compelidos a considerar um problema como resolvido apenas quando conduz às operações aritméticas principais. Dessa forma, o problema da redução seria colocado sob uma nova luz. Mas, para preencher o abismo entre a teoria colossal e a eficácia comparativamente pequena da matemática, é essencial ter uma compreensão realmente científica da unidade da teoria e prática, uma compreensão da primazia da prática sobre a teoria que a matemática burguesa adota. dia não, e não pode possuir. a criação de tais instrumentos nos daria novos logaritmos que nos permitiriam enfrentar problemas muito mais complicados do que podemos atualmente, quando somos compelidos a considerar um problema como resolvido apenas quando conduz às principais operações aritméticas. Dessa forma, o problema da redução seria colocado sob uma nova luz. Mas, para preencher o abismo entre a teoria colossal e a eficácia comparativamente pequena da matemática, é essencial ter uma compreensão realmente científica da unidade da teoria e prática, uma compreensão da primazia da prática sobre a teoria que a matemática burguesa adota. dia não, e não pode possuir. a criação de tais instrumentos nos daria novos logaritmos que nos permitiriam enfrentar problemas muito mais complicados do que podemos atualmente, quando somos compelidos a considerar um problema como resolvido apenas quando conduz às principais operações aritméticas. Dessa forma, o problema da redução seria colocado sob uma nova luz. Mas, para preencher o abismo entre a teoria colossal e a eficácia comparativamente pequena da matemática, é essencial ter uma compreensão realmente científica da unidade da teoria e prática, uma compreensão da primazia da prática sobre a teoria que a matemática burguesa adota. dia não, e não pode possuir. Dessa forma, o problema da redução seria colocado sob uma nova luz. Mas, para preencher o abismo entre a teoria colossal e a eficácia comparativamente pequena da matemática, é essencial ter uma compreensão realmente científica da unidade da teoria e prática, uma compreensão da primazia da prática sobre a teoria que a matemática burguesa adota. dia não, e não pode possuir. Dessa forma, o problema da redução seria colocado sob uma nova luz. Mas, para preencher o abismo entre a teoria colossal e a eficácia comparativamente pequena da matemática, é essencial ter uma compreensão realmente científica da unidade da teoria e prática, uma compreensão da primazia da prática sobre a teoria que a matemática burguesa adota. dia não, e não pode possuir.
O sexto abismo é o que existe na chamada fundação da matemática ou, mais exatamente, naquela superestrutura filosófica cuja finalidade é justificar todo o edifício, incorporá-lo ao sistema mundial como um todo. As duas filosofias rivais para a matemática burguesa atual, a logística e a intuicionista, são ambas idealistas. É indiferente se o mundo dos conceitos matemáticos é considerado como um mundo de universais imóveis rígidos, como é o caso dos logistas, ou se é visto como a esfera de ação do devir livre como é pelos intuicionistas. . É exatamente o mesmo se concordarmos com Russell que os conceitos matemáticos são a priori redutíveis à série natural que é dada completa em sua totalidade infinita, ou se assumimos com Weyl que os conceitos matemáticos nascem intuitivamente, não da percepção sensorial e da compreensão, mas de algum modo místico à parte do ser. A única filosofia, tão pouco quanto a outra, é capaz de resolver os paradoxos da teoria múltipla, a lei do meio excluído, a contradição entre o singular e o múltiplo e o finito e o infinito. As sutilezas mais refinadas do finitismo, da metalogia, da atomística matemática, apenas expressam a ansiedade dos matemáticos burgueses de se separarem da matéria e da dialética pelo véu da lógica formal, guiando-os diretamente para o deserto do escolasticismo. é capaz de resolver os paradoxos da teoria múltipla, a lei do meio excluído, a contradição entre o singular e o muitos, e o finito e o infinito. As sutilezas mais refinadas do finitismo, da metalogia, da atomística matemática, apenas expressam a ansiedade dos matemáticos burgueses de se separarem da matéria e da dialética pelo véu da lógica formal, guiando-os diretamente para o deserto do escolasticismo. é capaz de resolver os paradoxos da teoria múltipla, a lei do meio excluído, a contradição entre o singular e o muitos, e o finito e o infinito. As sutilezas mais refinadas do finitismo, da metalogia, da atomística matemática, apenas expressam a ansiedade dos matemáticos burgueses de se separarem da matéria e da dialética pelo véu da lógica formal, guiando-os diretamente para o deserto do escolasticismo.
Todas as profundas contradições da matemática - a contradição entre o singular e o múltiplo, entre o finito e o infinito, o discreto e o contínuo, o acidental e o necessário, o abstrato e o concreto, o histórico e o lógico, a contradição entre a teoria e a prática, entre a própria matemática e sua fundamentação lógica - todas são, na realidade, contradições dialéticas. Sua interpenetração e luta mútua realmente incorporam o desenvolvimento da matemática. Mas por causa da falta de plano para lidar com esses problemas, porque a anarquia reina na matemática burguesa como na ciência burguesa como um todo e em todo o sistema capitalista, porque não há e não pode haver nenhum planejamento geral, o processo de desenvolvimento matemático se encontra crises severas, experimenta períodos de estagnação e declínio. Isto é reforçado pela influência da filosofia da classe idealista e metafísica e pela extrema divisão do trabalho característica de toda a sociedade capitalista e que é particularmente evidente na matemática, onde é difícil encontrar um cientista capaz de entender trabalhos científicos que fazem não vem dentro de sua própria província estreita.
Para a matemática, há apenas uma saída: reconstrução consciente e planejada com base na dialética materialista. Será, no entanto, possível falar da reconstrução deliberada da matemática e da ciência como um todo, da introdução do planejamento na ciência, na matemática? O antigo preconceito sobre o que é chamado de obra científica criativa do indivíduo, decorrente da inspiração, foi destruído pelo próprio desenvolvimento da ciência. Sempre houve escolas científicas e o trabalho criativo de um indivíduo está firmemente enraizado no trabalho coletivo do todo. E no que diz respeito ao planejamento, sob o capitalismo, os grandes trustes estabelecem magníficos institutos de pesquisa organizados para o trabalho coletivo. Em qualquer caso, a própria história da matemática responde afirmativamente a essa questão. Klein ' s Programa Erlanger servirá como exemplo; este programa, apresentado em 1872, quando o capitalismo alemão estava crescendo e prosperando, realizou uma verdadeira revolução na geometria. Ela teve resultados extremamente frutíferos e é notável por se basear em uma idéia uniforme, a idéia de grupo, a idéia de um grupo de transformações espaciais e de descobrir os invariáveis que a caracterizam. O programa apresentado por Hilbert em 1900 foi muito menos bem sucedido do que o Programa Erlanger; não se baseia em uma idéia uniforme e é antes um índice de problemas separados - felizmente compreendidos, é verdade - de todos os ramos da matemática. Consequentemente, não realizou na matemática a revolução que o programa de Klein fez na geometria, embora, apesar de seu caráter de mosaico,
O programa Erlanger foi tão bem sucedido porque não é um programa matemático, mas sim um programa geométrico. A geometria, como uma ciência que é mais material que a matemática, não apenas se destacou menos da realidade do que a última, mas tem sido frequentemente de ajuda para ela. Os métodos e problemas geométricos tiveram um efeito benéfico sobre a matemática, atraindo-a de volta a "Uma mãe terra pecaminosa".
Isso não implica, no entanto, que a geometria tenha tido mais do que uma parte auxiliar para desempenhar, que já esteve em posição de assumir a parte principal da forma abstrata geral que a álgebra desempenha na matemática, que poderia dar mais do que a percepção intuitiva que ele dá. Este também é o ponto de vista a partir do qual temos de considerar o ramo mais recente da geometria, a topologia, que estuda as qualidades mais gerais das estruturas espaciais que permanecem inalteradas por quaisquer transformações contínuas e univalentes. Da topologia, em que uma certa síntese da constante e da variável (topologia da teoria do grupo e topologia da teoria de múltiplos) já foi conseguida e em que a escola de Alexandrov, Pontriagin (Moscou) e outros estão fazendo esforços conscientes para dar base lógica ao fato de que problemas topológicos foram levantados, uma série de métodos foram elaborados, fornecendo uma solução para problemas matemáticos que têm que ser compreendidos sinteticamente: estes são os métodos topológicos de Lusternik e Shnirelman como aplicados ao cálculo das variações. Espera-se que o estudo de métodos topológicos ajude indiretamente a matemática a progredir ainda mais nesse caminho.
Se os problemas enumerados acima devem ser resolvidos, como começar com o plano de reconstrução da matemática? A coisa mais simples, é claro, seria se alguém apresentasse um plano pronto, mas isso seria uma sentença de morte no plano em si, pois hoje em dia, a matemática tem tantos ramos, o plano que queremos só pode ser elaborado pelo trabalho coletivo. Tal plano, que pode ser feito apenas em um país onde a economia nacional e a ciência são planejadas, deve ser elaborado com base em toda a experiência adquirida em institutos de pesquisa científica e laboratórios de obras, com base nas exigências do indústria, agricultura e transporte de todo o país. Deveria, no entanto, ser mais do que um mero registro de temas sugeridos em conferências por cientistas e engenheiros;
Daí resulta que não podemos ignorar o que tem relação com a matemática e sua história nos escritos de Marx, Engels e Lênin. Devemos estudar cuidadosamente tudo sobre esse assunto em "Anti-Duhring" e "Naturdialektik", de Engels, em "Materialism and Empirio-Criticism", de Lênin, em seus escritos filosóficos e em várias outras obras, particularmente a econômica. Os escritos até então inéditos de Marx que tratam da matemática e sua história, dos quais existem mais de cinquenta e que em breve serão publicados pelo Instituto Marx-Engels (Moscou), são de tremenda importância metodológica.
A história das ciências matemáticas deve ser estudada à luz da teoria marxista-leninista, da filosofia do materialismo dialético e da questão das tendências em seu desenvolvimento trabalhadas em detalhes. Acima de tudo, temos que estudar o desenvolvimento da matemática na época do imperialismo e da revolução proletária, para continuar sobre uma base materialista-dialética a obra de Klein, o mais avançado dos matemáticos burgueses, em cujas obras descobrimos, além do Machismo, essencial constituintes do materialismo espontâneo. O trabalho de trazer esse volume está agora em andamento. Temos que concentrar nossa atenção no desenvolvimento dos principais conceitos matemáticos, particularmente sobre conceitos tão importantes como o quociente diferencial, o diferencial, o conceito limitante. Precisamos fazer uma classificação realmente científica das ciências matemáticas; temos que investigar a importância da álgebra como elo de conexão entre a aritmética e a análise, para estudar tais ramos "negligenciados" da matemática como, por exemplo, equações de diferenças finitas e sua conexão com a análise, ou séries divergentes; temos que descobrir por que, por enquanto, a matemática se afastou deles, temos que determinar a posição da teoria dos números na matemática, estudar seu desenvolvimento e o desenvolvimento de toda a estrutura das ciências matemáticas. equações de diferenças finitas e sua conexão com a análise, ou séries divergentes; temos que descobrir por que, por enquanto, a matemática se afastou deles, temos que determinar a posição da teoria dos números na matemática, estudar seu desenvolvimento e o desenvolvimento de toda a estrutura das ciências matemáticas. equações de diferenças finitas e sua conexão com a análise, ou séries divergentes; temos que descobrir por que, por enquanto, a matemática se afastou deles, temos que determinar a posição da teoria dos números na matemática, estudar seu desenvolvimento e o desenvolvimento de toda a estrutura das ciências matemáticas.
Além de todos esses problemas teóricos gerais, há vários outros, diretamente ligados à construção socialista na União Soviética, que podem ser incorporados em um programa de trabalho prático para matemáticos soviéticos.
Estamos agora considerando a organização de um instituto de cálculo para toda a União Soviética, cuja tarefa será elaborar novos métodos de cálculo, para resolver os problemas matemáticos que surgem em nossa indústria socialista, no sistema de transportes, na coletivização e na industrialização. agricultura; este instituto se tornará a equipe operacional para todo o trabalho matemático sendo conduzido pelas diferentes instituições de pesquisa científica em todo o país.
Um grupo de problemas que nossos matemáticos têm que resolver é apresentado pelos problemas estatísticos que são tão importantes na economia socialista planejada, questões de projetar e distribuir centros econômicos (cuja grande importância foi enfatizada por Lenin), de racionalizar o transporte de bens, etc. .
Um segundo grupo se preocupa com a padronização da produção, com a elaboração de formas e séries ótimas de produtos, com os problemas de correias de transmissão e matrizes que surgem na racionalização dos empreendimentos.
O terceiro grupo consiste em problemas que surgiram na elaboração dos melhores métodos topográficos e cartográficos correspondentes à taxa de construção socialista; isso tem uma importância colossal em um país como a União Soviética, com sua vasta riqueza natural que não foi investigada sob a economia capitalista predatória do czarismo.
Há também um quarto grupo de problemas menos abrangentes relacionados com as estatísticas do interior da Terra, com a indústria de construção em rápido desenvolvimento, a construção de aeronaves, etc.
É apenas uma economia socialista planejada que pode apresentar problemas matemáticos com tais problemas, exigindo a participação complexa de vários ramos da matemática (por exemplo, cálculo de probabilidade combinado com geometria diferencial, cálculo de probabilidade e cálculo de variação, ou cálculo de variação e teoria de números, etc., problemas matemáticos complexos ajustados à produção em massa matemática e máxima eficácia, juntamente com extenso trabalho científico de investigação teórica.Assim, planejar matemática não significa sufocar o trabalho criativo - significa que a matemática florescerá como pode fazer somente com o trabalho coletivo, tanto mais que as fileiras dos cientistas são inchadas por novos homens da classe trabalhadora, aos quais os portões das universidades e dos institutos de pesquisa têm sido amplamente abertos.
A importante questão de reorganizar o ensino de matemática em todas as etapas da educação, do ensino politécnico à universidade, não pode ser tratada aqui.
Para resolver todos esses problemas teóricos e práticos, superar a crise da matemática atual, reconstruí-la segundo linhas socialistas, é necessário um trabalho paciente e persistente, o trabalho coletivo de todos os matemáticos soviéticos e dos cientistas dos países capitalistas que desejam vá com a gente. Partindo da teoria leninista da unidade da teoria e prática, nós, na União Soviética, reconstruiremos as ciências matemáticas. Reconhecendo o princípio leninista de que as ciências não são imparciais, devemos colocar a matemática a serviço da construção socialista e, desta forma, salvá-la da decadência que é inescapável sob o capitalismo.
| Inclusão | 13/03/2019 |